Singularity Analysis and Modular Synthesis of Over-Constrained Spatial Mechanisms - A Case Study ...

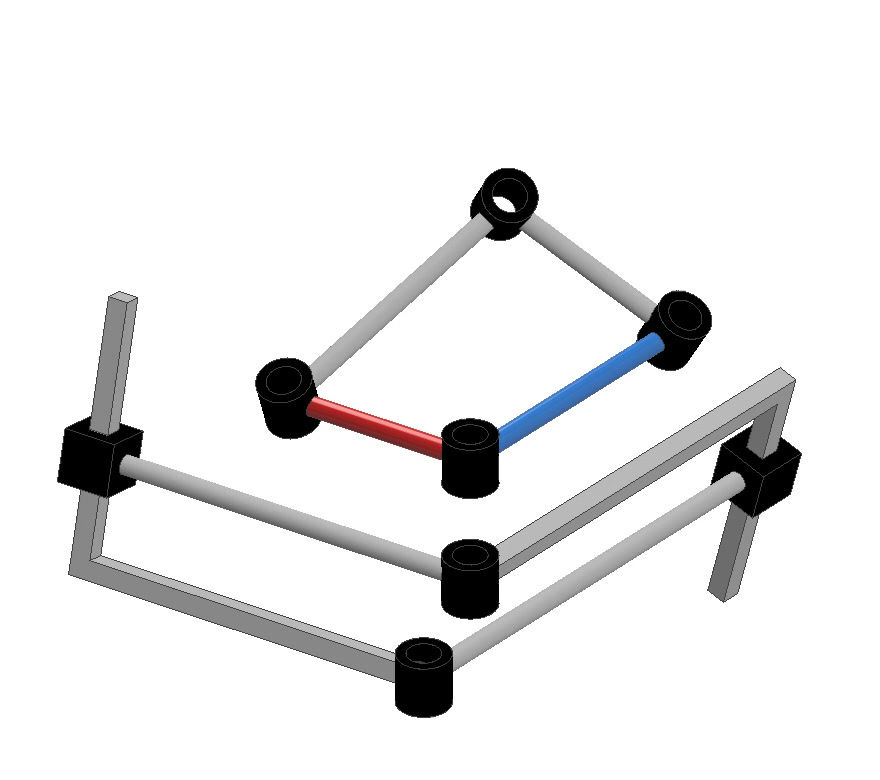
Singularity Analysis and Modular Synthesis of Over-Constrained Spatial Mechanisms - A Case Study on Bennett And RPRP Linkage

摘要
Geometric constraints of spatial RPRP linkages are comprehensively classified.
•Singularity analysis method is provided to find limited range of mechanism motion.
•Modular method is presented to synthesize a family of over-constrained mechanisms.

This paper revisits the geometric constraints for a movable spatial RPRP mechanism and further finds that it can be mobile as long as the link lengths and skew angles satisfy specific relationships, regardless of plane-symmetric property. Next, a set of kinematics analysis methods using D-H notations to analyze the modular mechanism are derived. In order to efficiently implement the concatenated over-constrained mechanism, this paper summarizes two singularity analysis methods based on Jacobian matrix form, square matrix or rectangular matrix, obtained by the velocity analysis to find the limited motion range of the mechanism. Then, this paper proposes a modular method to synthesize a family of spatial six-bar over-constrained mechanisms. In addition, by adjusting the geometric relationships between link lengths and skew angles, spatial six-bar over-constrained mechanisms can be further configured to a spatial five-bar or four-bar mechanisms. The modular method can effectively isolate a new concatenated six-bar mechanism synthesized from two different modular mechanisms, Bennett and spatial RPRP mechanisms, by removing overlapped links and joints. Furthermore, it is found that the concatenated mechanism retains the kinematics and singularity characteristics of the source mechanisms.